5. Operators

Operators perform mathematical or logical operations on values. The operators provided by UniScript are divided into three categories:

  • Arithmetic
  • Relational
  • Logical

Operators in UniScript can be applied on scalar values, vectors and matrices. The following matrices have special names:

Row * Column Name
1 * 1 scalar
1 * m row vector
n * 1 column vector
n * m matrix
n * n square matrix

5.1. Arithmetic Operators

5.1.1. Additive Operators

Most of the operators are performed on an element by element basis, e.g.:

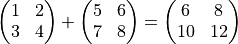
\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} = \begin{pmatrix} 6 & 8 \\ 10 & 12 \end{pmatrix}

The dimension of both operands must be equal. That means the number of rows and columns must be the same, except in the case where one operand is a scalar.

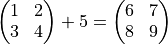
\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} + 5 = \begin{pmatrix} 6 & 7 \\ 8 & 9 \end{pmatrix}

or

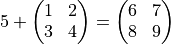
5 + \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} = \begin{pmatrix} 6 & 7 \\ 8 & 9 \end{pmatrix}

This is the only exception. Therefore, you cannot add a row vector to a column vector.

The + operator concatenates single strings to one string.

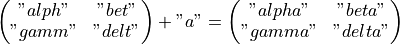
\begin{pmatrix} "alph" & "bet" \\ "gamm" & "delt" \end{pmatrix} + "a" = \begin{pmatrix} "alpha" & "beta" \\ "gamma" & "delta" \end{pmatrix}

Note:

["a", "b"] is a row vector with two elements,

"a" + "b" is the scalar string "ab".

5.1.2. Multiplication Operators

UniScript provides two multiplication operators: The matrix multiplication operator * and the multiplication operator .* for an element by element multiplication denoted by placing a period (.) ahead of the *.

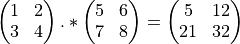
\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} .* \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} = \begin{pmatrix} 5 & 12 \\ 21 & 32 \end{pmatrix}

The * matrix multiplication operator requires that the second dimension of the first operand be the same as the first dimension of the second operand. Example:

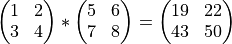
\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} * \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} = \begin{pmatrix} 19 & 22 \\ 43 & 50 \end{pmatrix}

If the first operand is a n * m matrix and the second operand is a m * q matrix, the resulting matrix will have the dimension n * q.

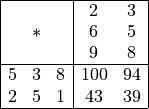
\begin{array}{|ccc|cc|} \hline & & & 2 & 3 \\ & * & & 6 & 5 \\ & & & 9 & 8 \\ \hline 5 & 3 & 8 & 100 & 94 \\ 2 & 5 & 1 & 43 & 39 \\ \hline \end{array}

5.1.3. Division Operators

UniScript provides three different matrix division operators. The ./ operator works on an element by element basis like the .* or the + operator.

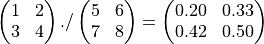
\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} ./ \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} = \begin{pmatrix} 0.20 & 0.33 \\ 0.42 & 0.50 \end{pmatrix}

The matrix division operator / (right-hand division) performs the operation

x / y = x * y^-1 = (y' \ x')' = ((y')^-1 * x')'.

If the system is not square, a minimum norm solution will be calculated.

The matrix left division x\y is equivalent to the expression x \ y = x^-1 * y, but it is computed without forming the inverse of x. Again, if the system is not square, a minimum norm solution will be calculated.

An example:

* a = [4,7;2,5]
* a
    4.0000   7.0000
    2.0000   5.0000
* b = [1;4]
* b
    1.0000
    4.0000
* x = a\b
* x
   -3.8333
    2.3333
* a * x
    1.0000
    4.0000
* a = [1,2;3,4;5,6]
* a
    1.0000   2.0000
    3.0000   4.0000
    5.0000   6.0000
* b = [7,8,9]'
* b
    7.0000
    8.0000
    9.0000
* x = a\b
* a * x // check
    7.0000
    8.0000
    9.0000

5.1.4. Modulus Operator

The % operator (which works like the + operator on an element by element basis) returns an integer value that is the remainder of an integer division.

In the first step, both operands will be converted to integers (5.9999 will result in the number 5):

* 5 % 2
    1.0000
* 5.999 % 2
    1.0000

5.1.5. Power Operator

For the power operation x^y, x must be a scalar or a square matrix and y must be a scalar. If y is an integer, the operation will be performed by multiplication. Otherwise, the operation will be performed by computing the eigenvalues and eigenvectors of x (with the matrix of eigenvectors and the diagonal matrix of the eigenvalues w).

* a = [1,2;3,4]
* a
    1.0000   2.0000
    3.0000   4.0000
* a^-1
   -2.0000   1.0000
    1.5000  -0.5000
* a*a^-1
    1.0000   0.0000
    0.0000   1.0000
* a^-1.1
   -2.1088 + 0.6974i     1.0366 - 0.3190i
    1.5549 - 0.4785i    -0.5539 + 0.2189i

The element wise power operator .^ works like the + operator on an element by element basis. That means that both operands need to have the same dimension or that one operand is a scalar.

5.1.6. Transpose Operator

This unary operator performs the matrix transpose operation. Both transpose operators ' and .' have the same result for real matrices. For a matrix with complex elements, a complex conjugate transpose operation is performed.

* a = [1,2;3,4]
* a
    1.0000   2.0000
    3.0000   4.0000
* a'
    1.0000   3.0000
    2.0000   4.0000
* a.'
    1.0000   3.0000
    2.0000   4.0000
* a = a + 3i
* a
    1.0000 + 3.0000i     2.0000 + 3.0000i
    3.0000 + 3.0000i     4.0000 + 3.0000i
* a'
    1.0000 - 3.0000i     3.0000 - 3.0000i
    2.0000 - 3.0000i     4.0000 - 3.0000i
* a.'
    1.0000 + 3.0000i     3.0000 + 3.0000i
    2.0000 + 3.0000i     4.0000 + 3.0000i

5.1.7. Summary

Operator Meaning
x + y Addition of real and complex numbers as well as concatenate strings.
x - y Subtraction of real and complex numbers.
x * y Matrix multiplication of real and complex numbers.
x .* y Multiplication of real and complex numbers.
x / y For scalars normal division. For matrices the division x/y is equivalent to the operation x * y^-1. If x is a scalar, x is divided by y on a element by element basis.
x ./ y Element by element division of real and complex numbers.
x y Left division. Computes the solution of the system x^-1 * y.
x % y Modulus arithmetic is denoted by the operator %. It gives the integer value that is the remainder of an integer division. Example: 10.4 % 2 is 2.
x ^ y Power operator for real and complex numbers.
x .^ y Element by element power operator for real and complex numbers.
x’ Transpose. The elements will be conjugated for complex matrices.
x.’ Transpose.

5.2. Comparison Operators

All comparison operators work on an element by element basis. The result of the comparison is either TRUE (1) or FALSE (0). This result can then be used to make decisions regarding program flow.

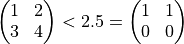
\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} < 2.5 = \begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}

Strings are compared lexicographically on a character by character base. Examples:

"a " == "a" is 0 (FALSE)

"a" < "b" is 1 (TRUE)

"Hello" == "hello" is 0 (FALSE)

In the first line, the left string contains blank characters. Tn the second line the character a is less than b. In the third line, the left string starts with a capital letter.

If you do not to want compare strings in this manner, you can use the functions strtrim and strlower (or strupper).

strtrim("a ") == strtrim("a") is 1 (TRUE)

strlower("Hello") == strlower("hello") is 1 (TRUE)

For complex numbers, only the operators == and != are defined.

Summary

Operator Meaning
x < y True if x is less than y.
x <= y True if x is less than or equal to y.
x == y True if x is equal to y.
x != y True if x is not equal to y.
x > y True if x is greater than y.
x >= y True if x is greater or equal to y.

5.3. Boolean Expressions

Boolean operators are often used in conjunction with comparison operators, as in the following example:

(a < 5) && (b > 8)

This expression returns 1 (TRUE) if a is less than 5 and b is greater than 8.

The AND operator (&&) has a lower precedence than all other comparison operators, therefore we do not have to use parentheses. But parentheses help to avoid precedence mistakes and should be used when you have an unusual combination.

Summary

Operator Meaning
x && y True if both x and y are true (AND).
x || y True if at least one of x or y is true (OR).
!x True if x is false (not x).

5.4. Bitwise Operators

UniScript uses the same binary operators as the programming language C. The bitwise operators perform the bitwise-AND (&), bitwise-exclusive-OR (@), and the bitwise-OR (|) operations.

The operands for bitwise operators must be of integer type. Therefore, the operands are converted to integers with 32 Bits. Example: 9.56 and 10.89 are first converted to 9 and 10. To perform a bitwise-AND operation, 9 & 10 can be expressed in binary as

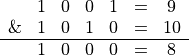
\begin{matrix} & 1 & 0 & 0 & 1 & =&9 \\ \& & 1 & 0 & 1 & 0 & =&10 \\ \hline & 1 & 0 & 0 & 0 & =&8 \end{matrix}

The bits in the result are 1 if the appropriate bits in the operands are 1, otherwise the bits are 0. The bitwise operators can be applied as the arithmetic + operator on vectors and matrices.

The bitwise-AND (&) operator is frequently used to set single bits to 0.

Example: rvSignal contains a signal from a 12-Bit data acquisition system. All bits of rvSignal should be set to 0 except for the lower 12 bits. This can be performed by an AND operation between rvSignal and 0x0FFF (rvSignal & 0x0FFF).

The bitwise-OR (|) operator compares each bit of its first operand to the corresponding bit of its second operand. If either bit is 1, the corresponding bit is set to 1, otherwise it is set to 0.

Example:

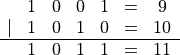
\begin{matrix} & 1 & 0 & 0 & 1 & =&9 \\ | & 1 & 0 & 1 & 0 & =&10 \\ \hline & 1 & 0 & 1 & 1 & =&11 \end{matrix}

The bitwise-exclusive-OR @ operator compares each bit of its first operand to the corresponding bit of its second operand. If one bit is 0 and the other bit is 1, the corresponding result bit is set to 1, otherwise it is set to 0.

Example:

\begin{matrix} & 1 & 0 & 0 & 1 & =&9 \\ @ & 1 & 0 & 1 & 0 & =&10 \\ \hline & 0 & 0 & 1 & 1 & =&3 \end{matrix}

The shift operator shifts the bits of the left operator to the left or to the right.

For example: The expression 01001 (binary) << 1 results in 10010 (binary) (this is equivalent to a multiplication by 2).

The bitwise-NOT (~) operator produces the bitwise complement of its operand.

Example:

~01001 (binary) is 10110 (binary).

Summary

Operator Meaning
x & y Bitwise AND operator.
x | y Bitwise OR operator.
x @ y Exclusive OR operator.
x << y Shift left.
x >> y Shift right.
~x Binary complement.

5.5. Operator Precedence

The following table lists UniScript operators in order of increasing precedence. Operators in the same row have the same precedence. To change the precedence of the operators, use parentheses or square brackets for index operations.

Example

* m1 = [1, 2]
* m2 = [3, 4]
* m3 = [5; 6]
* m = [m1;m2,m3]

>>> (E0000015) Operand format incompatible

* m = [[m1;m2],m3]
* m
    1.0000   2.0000  5.0000
    3.0000   4.0000  6.0000

The expression [m1;m2] must be enclosed in square brackets because the , operator has a higher precedence than the ; operator.

Operator Group order
= (assignment) right to left
; (column separator) left to right
, (row separator) left to right
|| (logical or) left to right
&& (logical and) left to right
| (binary or) left to right
@ (binary exclusive or) left to right
& (binary and) left to right
== != (comparison)left to right
<= < > >= > (comparison) left to right
<< >> (shift left, shift right) left to right
+ - (addition and subtraction) left to right
* .* / % ./ \ (multiplication) left to right
: (vector creation) left to right
! ~ - + (unary operators) left to right
^ .^ ' .' (power, transpose) right to left

id-2069568