Filterfunktionen für XY-Datensätze¶
Ab UniPlot 4.0 können für XY-Datensätze sogenannte Filterfunktionen definiert werden. Die Filterfunktionen sind eine Eigenschaft des Datensatzes und werden im Datensatz gespeichert. Wenn sich die Originaldaten des Datensatzes ändern, werden die Filterfunktionen neu berechnet, z. B. beim Datenaustausch oder wenn ein Datenpunkt interaktiv geändert wird. Im Diagramm werden die berechneten Daten graphisch dargestellt. Die Filterfunktion können für 1D- oder 2D-Datensätze definiert werden. Ein Datensatz kann eine oder mehrere Filterfunktionen enthalten. Die erste Funktion in der Liste verwendet als Eingangsdaten die Originaldaten des Datensatzes. Alle folgenden Funktionen greifen jeweils auf die Ergebnisdaten der vorherigen Filterfunktion zu. Das Ergebnis der letzten Filterfunktion wird graphisch dargestellt.
Die Ergebnisdaten der Berechnung werden im Datensatz gespeichert. Wenn Sie eine IPW-Datei weitergeben und eine Filterfunktion bei einem Anwender nicht vorhanden ist, wird der Datensatz zwar korrekt angezeigt, ein Austausch der Daten oder die Bearbeitung der Daten ist jedoch nicht möglich.
Die Filterfunktionen sind UniScript-Funktionen, die vom UniPlot-Anwender definiert werden können. Die folgenden Funktion können als Vorlage für eigene Filterfunktionen verwendet werden. Wie neue Filterfunktionen geschrieben werden, wird am Ende dieser Hilfeseite erklärt.
Liste der Filterfunktionen¶
Den Quellcode der folgenden Funktionen finden Sie in der Datei
script\rs_xy_ffunc.ic
Bei den Funktionen spline, fitspline, pspline und akimaspline kann für den Parameter nPoints die Zahl 0 angegeben werden. Die Funktion verwendet dann eine Anzahl an Stützstellen die abhängig von der Anzahl der Originaldatenpunkte n ist:
n |
nSplinePoints |
|---|---|
0-2 |
100 |
3-5 |
n*100 |
6-19 |
n*50 |
20-99 |
n*10 |
100-999 |
n*5 |
1000-100000 |
n*3 |
>=100000 |
n |
Grundlegende Filter¶
abs - Betrag¶
abs()
Berechnet den Betrag der y-Koordinaten.
cumsum - Kumulierte Summe¶
cumsum()
Kumulierte Summe der y-Koordinaten.
diff - Differenz¶
diff()
Diff berechnet die Differenz von aufeinanderfolgenden Datenpunkten.
y(i) = y(i+1)-y(i)
differentiate - Ableitung¶
differentiate()
Berechnet die Ableitung eines Datensatzes.
mean - Mittelwert¶
mean()
Mittelwert.
min - Minimumwert¶
min()
Berechnet das Minimum der y-Koordinaten.
max - Maximumwert¶
max()
Berechnet das Maximum der y-Koordinaten.
mean - Mittelwert¶
mean()
Berechnet den Mittelwert der y-Koordinaten.
median - Medianwert¶
median(nPercent)
Berechnet den Median der y-Koordinaten. Dazu werden die Daten in aufsteigender Folge sortiert und für nPercent=50 auf den Wert an der mittleren Stelle gesetzt. Der Index des Medianwerts wird aus der Punktanzahl multipliziert mit dem Prozentwert berechnet.
Integrate¶
integrate - Integral¶
integrate()
Berechnet den Integralverlauf mit Hilfe der Trapezmethode.
integrate_cycle - Integral (Zyklen)¶
integrate_cycle(xCycleLength, xCycleStart, nCycle)
Berechnet für jeden Zyklus den Integralverlauf mit Hilfe der Trapezmethode.
xCycleLength: Zykluslänge in X-Koordinaten, z. B. 0.2s oder 720 °KW.
xCycleStart: Zyklusbeginn in X-Koordianten, z. B. 0s oder -360 °KW.
xCycleStart wird auf den Wert von x[1] gesetzt, falls der Wert von xCycleStart kleiner als x[1] ist.
nCycle: Anzahl der Zyklen. 0 für alle Zyklen.
cycle_value - Integral (Zyklus/Wert)¶
cycle_value(Type, cycle_length, cycle_start, nCycle)
Berechnet für jeden Zyklus einen der folgenden Kennwerte: Mittelwert, Minimum oder Maximum.
nType kann einen der folgenden Werte annehmen:
1: Mittelwert
2: Maximum
3: Minimum
xCycleLength: Zykluslänge in X-Koordinaten, z. B. 0.2s oder 720 °KW.
xCycleStart: Zyklusbeginn in X-Koordinaten, z. B. 0s oder -360 °KW. xCycleStart wird auf den Wert von x[1] gesetzt, falls der Wert von xCycleStart kleiner als x[1] ist.
nCycle: Anzahl der Zyklen. 0 für alle Zyklen.
Skalierung¶
noise - Rauschen zufügen¶
noise(nNoiseInPercent, nMultPoints)
Fügt dem ausgewählten Datensatz Rauschen hinzu.
scale_x - Skalierung-X¶
scale_x(a,b)
Skaliert die x-Koordinaten nach der folgenden Gleichung x = a*x + b.
scale - Skalierung-Y¶
scale(a,b)
Skaliert die y-Koordinaten mit y = a*y + b.
correction_factor - Skalierung-Y (Berichtigungsfaktor)¶
correction_factor(x,y)
Korrigiert die y-Koordinate mit einem variablen Korrekturfaktor. Der Filter kann zur Korrektur von Sensorsignalen verwendet werden, von denen bekannt ist, dass sie in einigen Betriebspunkten abweichend sind.

characteristic_curve - Skalierung-Y (Charakteristische Kurve)¶
characteristic_curve(Page:Data Id)
Dieser Filter wandelt den Messwert eines Sensors anhand einer Kennlinie in seinen physikalischen Wert um. Bsp.: Spannung in bar für einen Drucksensor.
Seite: Seite der Kennlinie Daten-ID: Name des Datensatzes, der die Kennlinie enthält

Bit¶
bit - Bit-Extraktion und Konvertierung¶
Liefert das n-te Bit von y. nBit beginnt bei 1. Das Ergebnis kann skaliert werden.
bit(nBit, rsScaleFactor, rsScaleOffset)
nBit: Range 1 to 64
Skalierung: y = rsScaleFactor * (0/1-Wert) + rsScaleOffset;
Wenn rsScaleFactor auf 1 und rsScaleOffset auf 0 gesetzt ist, liegt das Ergebnis im Bereich von 0 bis 1.
Saubere Daten¶
remove_duplicate_points - Doppelte Datenpunkte entfernen¶
remove_duplicate_points()
Entfernt alle aufeinander folgende Punkte mit gleicher x-Koordinate bis auf den ersten Punkt.
remove_original_data_points - Originaldaten entfernen¶
remove_original_data_points()
Entfernt die Originaldaten aus dem Datensatz und setzt den Wert auf eine magische Zahl (x=0.123,y=0.456). Die Funktion kann dazu verwendet werden, um die IPW-Dateigröße zu reduzieren. Der Datenaustausch kann ausgeführt werden.
WICHTIG: Nachdem die Originaldaten entfernt wurden, werden die Filterfunktionen nicht mehr aktualisiert, außer beim Datenaustausch. Beispiel: Die Funktion kann z. B. in Verbindung mit der simplify Funktion verwendet werden:
simplify(5);remove_original_data_points()
Zum Speichern der Datei wählen Sie Datei=>Schließen und kompakt speichern.
Auszug Bereich¶
extract - Extrahiere Daten (X basiert)¶
extract(xmin, xmax)
Die Funktion extract schneidet alle Datenpunkte im X-Koordinatenbereich von xmin bis xmax aus. Die Punkte an den Grenzen xmin und xmax werden durch lineare Interpolation berechnet.
Die x-Koordinaten müssen dazu monoton steigend sein.
Siehe auch extract_points
extract_points - Extrahiere Daten (Punkt basiert)¶
extract_points(imin, imax)
Die Funktion extract_points schneidet einen Ausschnitt der Datenpunkte von imin bis imax aus.
imin: Erster Punkt (imin >= 1 und <= Anzahl Punkte - 2).
imax: Letzter Punkt. Falls für imax eine negative Zahl angegeben wird, wird von hinten gezählt, z. B. Punktanzahl ist 17:
extract_points(1,22) entspricht extract_points(1,17)
extract_points(1,-1) entspricht extract_points(1,17)
extract_points(1,0) entspricht extract_points(1,17)
extract_points(3,-3) entspricht extract_points(3,15)
peaks - Extrahiere Daten (Spitzen)¶
peaks(Threshold, bAbsolut, Type)
Der Filter Peaks wird verwendet, um lokale Maxima und Minima in einem verrauschten Signal zu finden. Um ihn zu verwenden, erstellen Sie eine Kopie des Signals (Strg+C Strg+V) und aktivieren Sie Marker und die Option „Marker für gefilterte Daten“.
Threshold: Wert zur Erkennung lokaler Extrema
bAbsolut: Einer der folgenden Werte:
0: Schwellenwert in Prozent des y-Datenbereichs
1: Schwellenwert in Einheiten der y-Daten
Typ: Typ ist einer der folgenden Werte.
1: Suche nach lokalen Maxima (Spitzenwerte)
2: Suche nach lokalen Minima (Tälern)
3: Suche nach lokalen Maxima und Minima
find - Extrahiere Daten (Spezial)¶
find(min, max, Axis, Type)
Liefert die Datenpunkte im Bereich von min bis max. Falls kein Datenpunkt im Bereich liegt, liefert die Funktion den Wert 0.
Axis ist einer der folgenden Werte:
1: Filter auf die x-Koordinaten anwenden.
2: Filter auf die y-Koordinaten anwenden.
Type ist einer der folgenden Werte:
0: Absolute Werte
1: Relative Werte: Werte werden vor dem Suchen durch den Maximalwert dividiert (xy / xymax).
2: Relative Werte: Werte werden vor dem Suchen auf den Bereich 0 bis 1 skaliert (xy - xymin) / (xymax-xymin).
Für den Type 1 oder 2 sollte min und max im Bereich 0 und 1 liegen.
Beispiel: Mit dem folgenden Filter können alle Punkte gesucht werden, deren y-Koordinaten im Bereich 90% vom Maximumwert liegen: find(0.9, 1.0, 2, 1).
Frequenz¶
fft_spectrum - FFT: Frequenzspektrum¶
fft_spectrum(iWindow, Segment_Points)
Berechnet das Spektrum eines Datensatzes mittels FFT.
Segment_Points: 0 (alle Punkte), 32, 64, 128, 256, etc.
iWindow ist einer der folgenden Werte:
0: Rectangular Window
1: Hanning Window
2: Hamming Window
3: Welch Window
4: Parzen Window.
5: FlatTop Window
6: Blackmann Window

fft_filter - FFT: Filter¶
fft_filter(rsFreqCutOffBelow, rsFreqCutOffAbove)
Bandpaßfilter. Alle Frequenzen unterhalb der Frequenz rsFreqCutOffBelow und oberhalb der Frequenz rsFreqCutOffAbove werden entfernt. Der Zeitkanal muss in Sekunden definiert sein. Die Frequenzen werden in der Einheit Hz (1/s) definiert.
Interpolation¶
interpol - Interpolation (Linear)¶
interpol()
interpol(nPoints)
Berechnet Zwischenpunkte durch lineare Interpolation.
nPoints: Anzahl der Punkte, die gleichmäßig über den x-Koordinatenbereich verteilt werden, oder eine Liste der x-Koordinaten durch Komma getrennt.
interpol2 - Interpolation (Lineare-min/max/delta)¶
interpol2(xmin, xmax, xdelta)
Berechnet Zwischenpunkte von xmin bis xmax in Schritten von xdelta durch lineare Interpolation.
Der Datensatz muss monoton sein. Falls xmin oder xmax außerhalb des x-Wertebereichs liegt, wird der Bereich entsprechend korrigiert, da die Funktion keine Extrapolation durchführt.
interpol_cosine - Interpolation (Cosinus)¶
interpol_cosine(nPoints)
Berechnet Zwischenpunkte durch Cosinus Interpolation.
nPoints: Anzahl der Punkte, die gleichmäßig über den x-Koordinatenbereich verteilt werden, oder eine Liste der x-Koordinaten durch Komma getrennt.
Glätten¶
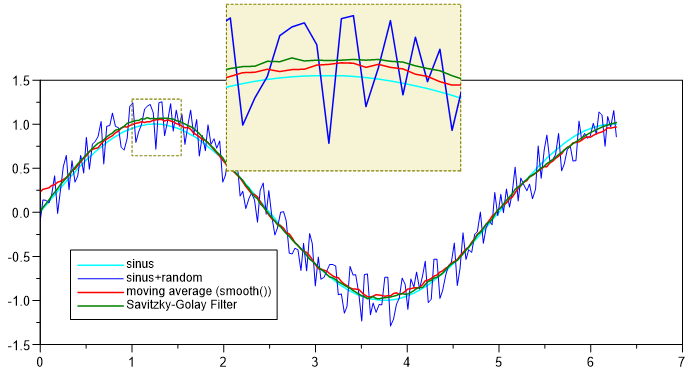
smooth - Glätten (gleitender Mittelwert)¶
smooth()
smooth(nNeighbor)
smooth(nNeighbor, PeakFilterFactor)
Glättet einen Datensatz mit dem gleitenden Mittelwert.
Der optionale Parameter nNeighbor gibt die Anzahl der Nachbarpunkte an, die
beim Glätten berücksichtigt werden. nNeighbor ist die halbe Fensterbreite.
Die gesamte Fensterbreite ist nNeighbor * 2 + 1.
Falls der Parameter nicht angegeben wird, wird nNeighbor gleich 10 gesetzt.
Mit Hilfe des optionalen Parameters PeakFilterFactor kann festgelegt werden,
wie die Spitzen in das gefilterte Signal übernommen werden sollen.
Default-Wert ist 0.
So funktioniert der Peak-Filter:
Die smooth-Funktion wird auf die Originaldaten angewendet.
Es wird die Differenz zwischen den Originaldaten und dem gefilterten Daten berechnet (= Abweichung).
Es wird das Maximum der Abweichung gesucht und mit dem neuen Faktor multipliziert (= dy).
Es werden alle Punkte in den Originalpunkten gesucht, deren Abweichung größer als dy sind.
Die gefunden Punkte werden in das geglättete Signal wieder eingefügt.
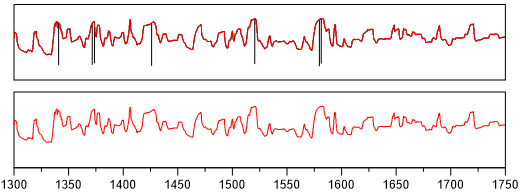
smooth_median - Glätten (gleitender Median)¶
smooth_median(nNeighbor)
Gleitender Median. nNeighbor ist die Fensterbreite im Bereich 3 bis 1025. Gerade Zahlen werden auf die nächste ungerade Zahl aufgerundet. Verwendet die Funktion moving_median.
Beispiel: smooth_median(5)
5 aufeinander folgende Punkte aufsteigend sortiert und der dritte Wert wird in den Ergebnisvektor geschrieben. Bei einer Fensterbreite von 5 Punkten werden die ersten zwei Punkte und die letzten zwei Punkte unverändert in den Ergebnisvektor geschrieben.
Gegeben: [5, 7, 6, 4, 27, 8, 4, 5]
Ergebnis: [5, 7, 6, 7, 6, 8, 4, 5]
Beispiel für Ausreißerfilterung:
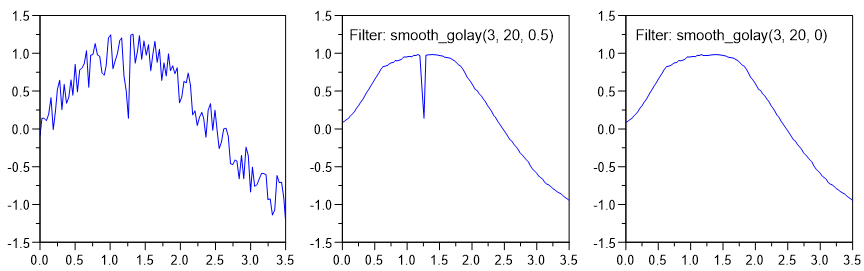
smooth_golay - Glätten (mit Savitzky-Golay Filter)¶
smooth_golay(nPolynomialOrder, nWindowSize)
smooth_golay(nPolynomialOrder, nWindowSize, PeakFilterFactor)
Die Punkte aus der Umgebung der Filterstelle werden für die Berechnung eines Ausgleichspolynoms verwendet (z. B. 5 Punkte für eine Ausgleichsparabel). Gegenüber dem gleitenden Mittelwert, erhält die Savitzky-Golay-Glättung besser die Form von Peaks. Die Höhe des Peaks wird weniger reduziert und die Breite weniger vergrössert. Allerdings ist auch hier der Einfluss auf die Peakhöhe bzw. die Peakfläche von der ursprünglichen Peakbreite und Peakform abhängig.
Glättung mit Peak-Filter. Die Funktionsweise entspricht dem smooth-Filter.
smooth_time - Glätten (mit Zeitfenster)¶
smooth_time(rsTimeWindow)
Glättung mit gleitendem Mittelwert. Ein Punkt p des Polygons wird berechnet, indem der Punkt p und n Nachbarpunkte davor und danach arithmetisch gemittelt werden. Mean_i = sum(i-n .. i+n) / (2*n+1)
rsTimeWindow ist die Länge des Zeitfensters, das für die Mittelung verwendet werden soll. Die Funktion berechnet aus der Länge die Anzahl der Datenpuntke n im Zeitfenster.Die Daten müssen mit konstanter Frequenz aufgenommen sein.
Polynom Fit¶
spline - Spline (Kubisch)¶
spline()
spline(nPoints)
Berechnet einen kubischen Spline, der alle Datenpunkte schneidet.
nPoints: Anzahl der Punkte des Splines. Die Anzahl muss im Bereich von 10 bis 100000 liegen.
nPoints = 0: Anzahl der Punkte automatisch bestimmen (siehe oben).
fitspline - Spline (fitspline)¶
fit_spline()
fit_spline(smoothfactor)
fit_spline(smoothfactor, nPoints)
Ausgleichsspline. Die Funktion berechnet einen Spline, der eine Glättung durchführt.
smoothfactor: Glättungsfaktor. Ein Wert von 0 ergibt keine Glättung (d.h. alle Punkte des Splines gehen durch die Originaldatenpunkte) und ein Wert größer als 0 führt eine Glättung durch.
nPoints: Punktanzahl (10 bis 100000).
nPoints = 0: Anzahl der Punkte automatisch bestimmen (siehe oben).
akimaspline - Spline (Akima)¶
akimaspline()
akimaspline(nPoints)
Kubischer Spline der gut mit diskontinuierlichen Änderungen zurecht kommt, ohne zu stark überzuschwingen. Die Akimainterpolationsmethode verzichtet gegenüber rein kubischen Splines auf die Stetigkeit der zweiten Ableitung.
nPoints: Anzahl der Punkte des Splines. Die Anzahl muss im Bereich von 10 bis 100000 liegen.
nPoints = 0: Anzahl der Punkte automatisch bestimmen (siehe oben).
rspline - Spline (Rational)¶
rspline(nPoints, TensionFactor)
Rationale Spline-Interpolation, die besser mit Unstetigkeiten in einer Zeitreihe zurechtkommt.
nPoints: Anzahl der Splinepunkte im Bereich von 10 bis 100000.
TensionFactor: Parameter zur Begradigung der Kurve (0 bis 100).
pspline - Spline (Parameter Spline)¶
pspline(f, nPoints)
Wenn f nahezu Null ist (z. B. 0,001), ist die resultierende Kurve annähernd ein kubischer Spline. Wenn f groß ist (z. B. 50), ist die resultierende Kurve annähernd eine polygonale Linie.
f: Faktor für die Spannung.
nPunkte: Anzahl der Punkte (3 bis 100000). nPoints = 0: Automatische Erstellung der Anzahl der Punkte.
oldspline - Spline (alte Version)¶
oldspline()
Berechnet einen kubischen Spline, der alle Datenpunkte schneidet. Diese Funktion
existiert aus Kompatibilitätsgründen zu UniPlot 3.x. Verwenden Sie statt dessen
die Funktion spline(0).
polyfit - Polynomfit¶
polyfit()
polyfit(polynomOrder)
polyfit(polynomOrder, nPoints, nInfoText)
polyfit(polynomOrder, nPoints, nInfoText, xMin, xMax)
Erzeugt ein Ausgleichspolynom 0ter bis 9terOrdnung, wobei order=1 eine Ausgleichsgerade ergibt (Regressionsgerade).
polynomOrder: Ordnung des Polynoms (Default = 1).
nPoints: Anzahl der Punkte, aus denen die Kurve gebildet werden soll (Default = 1000). Die Punktanzahl muss im Bereich 2 bis 100000 liegen.
nInfoText:
0 = kein Text.
1 = Polynomparameter.
2 = Polynomparameter und R2 (Bestimmtheitsmaß)
xMin: Startwert. Kann kleiner als der erste Datenpunkt sein. Falls der Wert auf 1e10 gesetzt wird, wird der erste Datenpunkt verwendet.
xMax: Endwert. Kann größer als der letzte Datenpunkt sein. Falls der Wert auf 1e10 gesetzt wird, wird der letzte Datenpunkt verwendet.
polyfitzero - Polynomfit (Y-Achsenabschnitt bei 0)¶
polyfitzero()
polyfitzero(polynomOrder)
polyfitzero(polynomOrder, nPoints, nInfoText)
Die Funktion berechnet ein Ausgleichspolynom (Fit), dass den Ursprung schneidet (y-Achsenabschnitt = 0).Erzeugt ein Ausgleichspolynom 0ter bis 9ter Ordnung, wobei n=1 eine Ausgleichsgerade ergibt (Regressionsgerade).
polynomOrder: Ordnung des Polynoms
nPoints: Anzahl der Datenpunkte (Default=1000)
nInfoText:
0 = Kein Textobjekt anzeigen.
1 = Textobjekt mit Polynom Parameter anzeigen.
2 = Textobjekt mit Polynom Parameter anzeigen und R2 (Bestimmtheitsmaß) anzeigen.
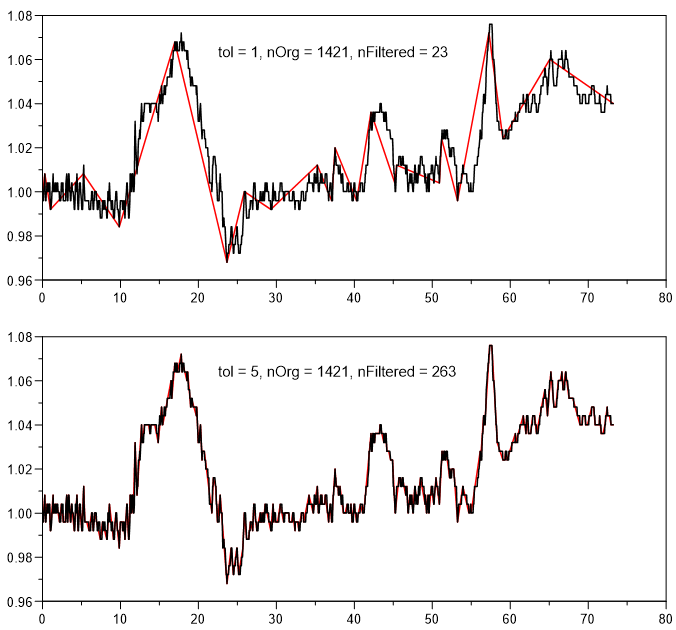
simplify - Simplify¶
simplify()
simplify(nTolerance)
Datenpunkt-Reduzierung mit dem Douglas-Peucker Verfahren.
nTolerance: gleich 1 bedeutet, dass alle Punkte der transformierten Kurve höchstens einen Abstand von 10% zur Originalkurve haben. Die Werte 2, 3, 4 bis 30 halbieren die Tolerenz. 4 ist also ein Abstand von 1.25%, bei 20 ist der Abstand nahezu 0. Default-Wert ist 5.
Erweiterte¶
boundary - Hüllkurve erzeugen¶
boundary()
boundary(type)
boundary(type, width)
Berechnet die obere, untere oder obere und untere Hüllkurve, die die Daten einschließt.
type
0 - obere Hüllkurve (Defaultwert: 0).
1 - untere Hüllkurve.
2 - obere und untere Hüllkurve.
width: Klassenbreite in Prozent (Defaultwert 5%).
center - Zentrum einer Punktwolke bestimmen¶
center()
Zentrum einer Punktwolke bestimmen. Berechnet den Mittelwert aller x- und y-Koordinaten. Der Mittelpunkt wird durch ein Symbol markiert.
Wichtig: Marker für gefilterte Daten einstellen!
convex_hull - Konvexe Hülle¶
convex_hull()
Ermittelt die konvexe Hülle eines Datensatzes.
event_duration - Dauer der Veranstaltung¶
event_duration()
Berechnet die Dauer aller hohen Ereignisse eines booleschen Signals und gibt einen Datensatz aus, wobei:
X: Beginn des Ereignisses
Y: Dauer des Ereignisses
Das folgende Beispiel zeigt eine typische Verwendung dieses Filters.
Wenden Sie einen find Filter auf eine Kurve an, um bestimmte Ereignisse anzuvisieren
min = 0
max = 0.7
Axis = 2
Type = 3 (1, wenn die Min/Max-Bedingung erfüllt ist, sonst 0)
Anwendung eines Filters event_duration zur Berechnung der Dauer.
Rechts-Klick => Textobjekt => 2D-Tabelle um eine Tabelle aus dem Datensatz zu erhalten.
Fügen Sie der Tabelle eine bedingte Formatierung hinzu, um benötigte Informationen schnell hervorzuheben. Informationen hervorzuheben.

histogram - Histogramm¶
histogram(Type, ClassMin, ClassMax, ClassWidth)
Berechnet ein Histogramm.
Falls ClassMin=0 und ClassMax=0 ist, wird die Klassenbreite ClassWidth als Anzahl der Klassen im y-Bereich verwendet
Type kann einer der folgenden Werte sein:
1: Absolut
2: Prozent
3: kumulativ (‚mehr als‘)
4: kumulativ in Prozent (‚mehr als‘)
5: kumulativ (‚weniger als‘)
6: kumulativ in Prozent (‚weniger als‘)

Siehe auch histogram
range_counting - Spannenverfahren (DIN 45667)¶
range_counting(rsThreshold)
Spannenverfahren (Range counting) nach DIN 45667.
DIN 45667: Classification methods for evaluation of random vibriations. Als Spannen werden die Differenzen zwischen zwei benachbarten Extremwerten bezeichnet. Die sortierten Spannen werden ausgegeben.
Um ein Histogramm von den Spannen zu erzeugen wählen Sie die Funktion histogram() aus.
Parameter:
rsThreshold: Nur Spannen, die größer als der Grenzwert sind, werden berücksichtigt.
nType
1: Alle Amplituden (Positive und negative)
2: Nur positive Spannen
3: Nur negative Spannen

set_to_zero - Über dem Schwellenwert auf 0 gesetzt¶
set_to_zero(rsThreshold)
Setzt eine Kurve auf 0 , wenn ein Schwellwert überschritten wird.
sort - Sortiere aufsteigend¶
sort()
Sortiert die Datenpunkte nach der x-Koordinate.
step - Step¶
step()
step(nType)
Berechnet eine Stufen-Kurve (z. B. Cityscape or Skyline).
nType kann einen der folgenden Werte annehmen:
0 - Kurve beginnt horizontal.
1 - Kurve beginnt vertikal (Defaultwert = 1).
to1d - x/y => t/y (1D)¶
to1d()
Wandelt einen x/y-Datensatz in einen t/y-Datensatz um. Die x-Koordinaten werden dabei über den gesamten x-Koordinatenbereich gleichmäßig verteilt.
Schreiben eigener Filterfunktionen¶
Das Schreiben einer Filter-Funktion soll an einem Beispiel gezeigt werden.
def _xy_filter_func_scale(hData, a, b)
{
if (nargsin() == 1) {
_a = 1;
_b = 0;
} else if (nargsin() == 2) {
_a = a;
_b = 0;
} else if (nargsin() == 3) {
_a = a;
_b = b;
}
xy = XYGetData(hData);
x = xy[;1];
y = xy[;2];
y = _a * y + _b;
return XYSetData(hData, x, y, TRUE); // TRUE ist wichtig!
}
def _xy_filter_info_scale()
{
svInfo = ["Y-Skalierung";
"scale(a,b)\n\nSkalierung der y-Koordinaten mit Hilfe" + ....
"der Geradengleichung y = a*y + b";
"";
"2";
"Skalierungswert a:1:-1e9:1e9";
"Verschiebungswert b:0:-1e9:1e9"];
return svInfo;
}
Um eine neue Filterfunktion zu definieren, müssen zwei Funktionen geschrieben
werden. Eine Funktion berechnet die Daten, die andere Funktion stellt
Informationen für die Benutzerschnittstelle bereit. Bei dem oben gezeigten
Beispiel sind das die Funktionen _xy_filter_func_scale und
_xy_filter_info_scale.
Die Namen von Filterfunktionen fangen mit den Zeichenfolge _xy_filter_func_
an, gefolgt von dem Anwender-Namen der Filterfunktion, in diesem Beispiel
scale.
Die Funktionen können in einer Datei mit der Endung .ic im
autoload-Verzeichnis von UniPlot gespeichert werden. Beim Start von UniPlot
werden die Funktionen dann automatisch geladen.
Die Info-Funktion gibt einen Stringvektor mit mindestens 4 Elementen zurück.
Element |
Bedeutung |
|---|---|
svInfo[1] |
Name der Funktion. |
svInfo[2] |
Beschreibungstext der im Hilfefenster angezeigt wird. Falls der Text länger ausfällt, kann man wie im Beispiel den Text auf mehrere Zeilen verteilen. Die Zeilen werden dann mit |
svInfo[3] |
Nicht benutzt. Muss ein leerer String sein („“). |
svInfo[4] |
Anzahl der Parameter „0“ bis „8“ |
svInfo[5] |
Hinter svInfo[4] folgen 0 bis 8 weitere Info-Strings. Sie enthalten den Namen des Parameters, gefolgt von 3 durch Doppelpunkte getrennte Zahlen. Die erste Zahl ist der Defaultwert, gefolgt von einem Minimum- und einem Maximum-Wert, den der Parameter annehmen kann. Beispiel: |
Die Func-Funktion führt die Berechnung durch. Als erster Parameter wird immer der Handle des Datensatzes übergeben. Über den Handle kann auf die Daten des Datensatzes zugegriffen werden (XYGetData). Die Ergebnisdaten werden mit der Funktion XYSetData zurückgeschrieben. Die weiteren Parameter sind optional.
History
Version |
Beschreibung |
|---|---|
R2024.4 |
xy_filter_event_duration Berichtigung |
R2024.3 |
|
R2022.2 |
id-1866448