5. Operatoren¶
Operatoren wie der Additionsoperator + können in UniScript auf skalare
Größen, Vektoren und Matrizen angewendet werden. Folgende Matrizen haben einen
speziellen Namen:
| Zeile * Spalte | Name |
|---|---|
| 1 * 1 | Skalar |
| 1 * m | Zeilenvektor |
| n * 1 | Spaltenvektor |
| n * m | Matrix |
| n * n | quadratische Matrix |
5.1. Arithmetische Operatoren¶
5.1.1. Additions-Operator¶
Die meisten Operatoren wirken elementweise, z. B.
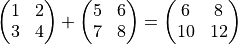
In diesem Fall müssen beide Operanden das gleiche Format haben, d. h. die gleiche Anzahl an Zeilen und Spalten. Jedoch kann einer der beiden Operanden ein Skalar sein:
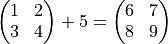
oder
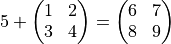
Andere Ausnahmen gibt es nicht, insbesondere kann kein Zeilenvektor zu einem Spaltenvektor addiert werden.
Bei Zeichenketten wirkt der +-Operator wie eine Verkettung.
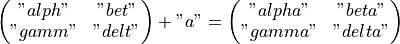
Man beachte den Unterschied:
["a", "b"] ist ein Zeilenvektor mit zwei Elementen aus jeweils einem Zeichen.
"a" + "b" ist der Skalar "ab", der aus zwei Zeichen besteht.
5.1.2. Multiplikations-Operator¶
In UniScript gibt es zwei verschiedene Multiplikationsoperatoren: Den
Matrizen-Multiplikations-Operator * und den elementweisen
Multiplikations-Operator .*, der aus den beiden Zeichen . und *
besteht, die unmittelbar hintereinander stehen müssen.
Der .*-Operator wirkt wie der +-Operator elementweise:
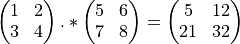
während der *-Operator eine echte Matrizenmultiplikation durchführt:
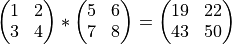
Wenn einer der beiden Operanden ein Skalar ist, liefern beide Multiplikationsarten das gleiche Ergebnis.
Bei Matrix-Multiplikationsoperatoren gilt nicht, daß die Zeilenanzahl gleich der Spaltenanzahl sein muss, sondern die Spaltenanzahl der ersten Matrix muss gleich der Zeilenanzahl der zweiten Matrix sein, was man gut erkennt, wenn man die Matrizen nach dem Falkschen Schema aufschreibt:
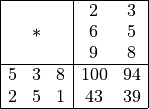
Eine n * m-Matrix multipliziert mit einer m * q-Matrix
liefert eine n * q-Matrix.
5.1.3. Divisions-Operator¶
Es gibt drei verschiedene Divisionsoperatoren. Die elementweise
Division ./ arbeitet wieder ähnlich wie die Addition:
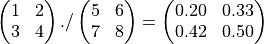
während die Matrix-Division x/y (Rechts-Division) der Operation
x / y = x * y^-1 = (y' \ x')' = ((y')^-1 * x')'
entspricht. Falls das System nicht quadratisch ist, wird eine
Minimum-Norm-Lösung berechnet.
Die Matrix-Links-Division x\y entspricht der Operation
x \ y = x^-1 * y, ohne daß jedoch intern die Inverse
berechnet wird. Auch bei diesem Operator gilt, daß falls das System
nicht quadratisch ist, eine Minimum-Norm-Lösung berechnet wird.
Beispiel:
* a = [4,7;2,5]
* a
4.0000 7.0000
2.0000 5.0000
* b = [1;4]
* b
1.0000
4.0000
* x = a\b
* x
-3.8333
2.3333
* a * x
1.0000
4.0000
* a = [1,2;3,4;5,6]
* a
1.0000 2.0000
3.0000 4.0000
5.0000 6.0000
* b = [7,8,9]'
* b
7.0000
8.0000
9.0000
* x = a\b
* a * x // Probe
7.0000
8.0000
9.0000
5.1.4. Modulus-Operator¶
Der %-Operator (der wie der +-Operator elementweise wirkt)
bestimmt den ganzzahligen Rest einer Division. Zunächst werden beide
Zahlen durch Abschneiden der Nachkommastellen in ganze Zahlen
umgewandelt. 5.999 wird dadurch in die Zahl 5 umgewandelt. Beispiel:
* 5 % 2
1.0000
* 5.999 % 2
1.0000
5.1.5. Power Operator¶
Bei der Potenzierung x^y muss x ein Skalar oder eine
quadratische Matrix sein und y ein Skalar sein. Falls y eine
ganze Zahl ist, wird die Operation durch Multiplikationen
durchgeführt, sonst über die Eigenwerte und Eigenvektoren von x
(x * omega^y * x^-1) mit der Matrix der Eigenvektoren x und der
Diagonalmatrix der Eigenwerte omega).
* a = [1,2;3,4]
* a
1.0000 2.0000
3.0000 4.0000
* a^-1
-2.0000 1.0000
1.5000 -0.5000
* a*a^-1
1.0000 0.0000
0.0000 1.0000
* a^-1.1
-2.1088 + 0.6974i 1.0366 - 0.3190i
1.5549 - 0.4785i -0.5539 + 0.2189i
Der elementweise Potenz-Operator .^ wirkt wie der +-Operator,
d.h. entweder haben beide Operanden das gleiche
Format, oder einer der beiden Operanden ist ein Skalar.
5.1.6. Transpositions-Operator¶
Die beiden Transponierungs-Operatoren '
(Transponierung) und .' haben bei reellen Matrizen die
gleiche Wirkung. Bei Matrizen mit komplexen Elementen werden die
Elemente beim '-Operator jedoch zunächst konjugiert.
* a = [1,2;3,4]
* a
1.0000 2.0000
3.0000 4.0000
* a'
1.0000 3.0000
2.0000 4.0000
* a.'
1.0000 3.0000
2.0000 4.0000
* a = a + 3i
* a
1.0000 + 3.0000i 2.0000 + 3.0000i
3.0000 + 3.0000i 4.0000 + 3.0000i
* a'
1.0000 - 3.0000i 3.0000 - 3.0000i
2.0000 - 3.0000i 4.0000 - 3.0000i
* a.'
1.0000 + 3.0000i 3.0000 + 3.0000i
2.0000 + 3.0000i 4.0000 + 3.0000i
Zusammenfassung
| Operator | Bedeutung |
|---|---|
x + y |
Addition von reellen und komplexen Zahlen sowie Verkettung von Strings. |
x - y |
Subtraktion von reellen und komplexen Zahlen. |
x * y |
Matrizen-Multiplikation von reellen und komplexen Zahlen. |
x .* y |
Elementweise Multiplikation von reellen und komplexen Zahlen. |
| x / y | Bei Skalaren gewöhnliche Division. Bei Matrizen entspricht die Division
x/y der Operation x \* y^-1. Falls x ein Skalar ist, wird x
elementweise durch y geteilt. |
| x ./ y | Elementweise Division von reellen und komplexen Zahlen. |
x \ y |
Links-Division. Löst die Gleichung x^-1 \* y. |
x % y |
(Modulus) Ganzzahligen Rest einer Division bestimmen. Der Operator kann nur auf reelle Zahlen angewendet werden. |
x ^ y |
Potenzierung von reellen und komplexen Zahlen. |
x .^ y |
Elementweise Potenzierung von reellen und komplexen Zahlen. |
| x‘ | Transponierung. Bei komplexen Matrizen werden die Elemente konjugiert. |
| x.‘ | Elementweise Transponierung. |
5.2. Vergleichsoperatoren¶
Alle Vergleichsoperatoren wirken elementweise. Sie liefern 1, wenn der Vergleich wahr ist und 0, wenn der Vergleich falsch ist.
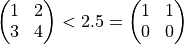
Bei Zeichenketten wird ein lexikographischer Vergleich durchgeführt:
"a" < "b" ist 1
Achtung: Zeichenketten mit Umlauten werden nicht nach deutschen lexikalischen Regeln verglichen.
Die Zeichenketten werden exakt und Zeichen für Zeichen verglichen. Z. B. ist:
"a " == "a" ist 0
"Hallo" == "hallo" ist 0
Im ersten Beispiel werden die Leerzeichen berücksichtigt und im zweiten Beispiel die Groß/Klein-Schreibweise. Ist das Verhalten nicht erwünscht, können die Funktionen strtrim und strlower (oder strupper) auf die Operanden angewendet werden.
strtrim("a ") == strtrim("a") ist 1
strlower("Hallo") == strlower("hallo") ist 1
Auf komplexe Zahlen können nur die beiden Operatoren == und
!= angewendet werden.
Zusammenfassung:
| Operator | Bedeutung |
|---|---|
| x < y | x kleiner y |
| x <= y | x kleiner oder gleich y |
| x == y | x gleich y |
| x != y | x ungleich y |
| x > y | x größer y |
| x >= y | x größer oder gleich y |
5.3. Boolsche Operatoren¶
Die boolschen (logischen) Operatoren werden meist in Verbindung mit den Vergleichsoperatoren angewendet. Z. B. ist der Ausdruck
(a < 5) && (a > 8)
wahr, d.h. gleich 1, wenn a kleiner als 5 und größer
als 8 ist.
Der Und-Operator hat eine niedrigere Priorität als alle
Vergleichsoperatoren, so daß der Ausdruck eigentlich nicht geklammert
werden müßte: a < 5 && a > 8 ist dasselbe wie
(a < 5) && (a > 8).
Zusammenfassung:
| Operator | Bedeutung |
|---|---|
| x && y | Logische Und-Verknüpfung. |
| x || y | Logische Oder-Verknüpfung. |
| !x | Logische Negation (Nicht x). |
5.4. Bitweise Operatoren¶
UniScript verfügt über die gleichen Operatoren für Bit-Manipulationen über die auch die Programmiersprache C verfügt.
Die Operanden werden zunächst durch Abschneiden in vorzeichenbehaftete
ganze Zahlen mit 32 Bits umgewandelt. Beispiel: 9.56 & 10.89 wird
bewertet als 9 & 10. Schreibt man die beiden Zahlen als Bitmuster
(binär) auf, erhält man
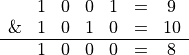
Die Bits im Ergebnis sind 1, wenn die entsprechenden Bits der
Operanden 1 sind und sonst 0. Die bitweisen Operatoren können wie der
arithmetische +-Operator auf Matrizen und Vektoren angewendet
werden.
Der Und - Operator wird dabei häufig dazu verwendet, einzelne Bits auf 0 zu setzen.
Beispiel: rvSignal enthält ein mit einem 12Bit-AD-Wandler
aufgenommenes Signal. Es sollen alle Bits von rvSignal bis auf
die unteren 12 Bits auf 0 gesetzt werden. Dies wird mit erreicht
indem man rvSignal mit 0x0FFF Und verknüpft
rvSignal & 0x0FFF.
Der Oder - Operator setzt die Bits auf 1, die in einem der Operanden 1 sind
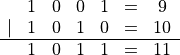
Der Exklusiv-Oder - Operator setzt die Bits auf 1, die in genau einem der Operanden 1 sind
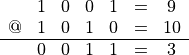
Die Schiebe-Operatoren schieben die Bits des linken Operanden
nach rechts oder links. Beispielsweise ergibt 01001 (binär) << 1
das Ergebnis 10010 (binär) (dies entspricht einer
Multiplikation mit 2). Die binäre Schreibweise ist in UniScript nicht
möglich. Sie dient hier nur zur Verdeutlichung.
Der Komplementoperator (ein Vorzeichen-Operator) vertauscht alle Bits
seines Operanden (~01001 (binär) ist 10110 (binär)).
Zusammenfassung:
| Operator | Bedeutung |
|---|---|
| x & y | Bitweise Und-Verknüpfung. |
| x | y | Bitweise Oder-Verknüpfung. |
| x @ y | Exklusiv-Oder-Verknüpfung. |
| x << y | Bitweises Links-Schieben. |
| x >> y | Bitweises Rechts-Schieben. |
| ~x | Bitweises Komplement. |
5.5. Assoziativität und Priorität der Operatoren¶
In der Tabelle auf der nächsten Seite ist die Assoziativität
(Zusammenfassung, Reihenfolge) und die Priorität (Vorrang) der
Operatoren in aufsteigender Reihenfolge angegeben. Operatoren in einer
Zeile haben den gleichen Vorrang. Durch Verwendung von Klammern bzw.
durch Zuweisung an temporäre Variablen kann die Reihenfolge der
Bewertung geändert werden. Mit „Klammern“ sind nicht unbedingt
die runden Klammern () gemeint.
Beispiel:
* m1 = [1, 2]
* m2 = [3, 4]
* m3 = [5; 6]
* m = [m1;m2,m3]
>>> (E0000015) Format der Operanden inkompatibel
* m = [[m1;m2],m3]
* m
1.0000 2.0000 5.0000
3.0000 4.0000 6.0000
Hier musste [m1;m2] geklammert werden, da der ,-Operator eine höhere
Priorität hat als der ;-Operator.
| Operatoren | Assoziativität |
|---|---|
= |
(Zuweisung) von rechts |
; |
(spaltenweise Verkettung) von links |
, |
(zeilenweise Verkettung) von links |
|| |
(logisches Oder) von links |
&& |
(logisches Und) von links |
| |
(bitweises Oder) von links |
@ |
(bitweises Exklusiv-Oder) von links |
& |
(bitweises Und) von links |
== != |
(Vergleich) von links |
<= < > >= |
(Vergleich) von links |
<< >> |
(Links- und Rechtsschieben) von links |
+ - |
(Addition und Subtraktion) von links |
* .* / % ./ \ |
(multiplikative Operatoren) von links |
: |
(Vektorerzeugung) von links |
! ~ - + |
(Vorzeichenoperatoren) von links |
^ .^ ' .' |
(Potenz, Transponierung) von rechts |
id-2069568